C5 Die Desynchronisation im Epstein-Diagramm
Uhren, die für Rot synchronisiert sind, projizieren auf dieselbe Stelle der roten Zeitachse. Für Rot synchronisierte Uhren liegen also auf Parallelen zur roten Raumrichtung. Für Schwarz, der alle Zeiten auf seiner schwarzen Zeitachse abliest, weisen aber solche Uhren eine Zeitdifferenz auf:
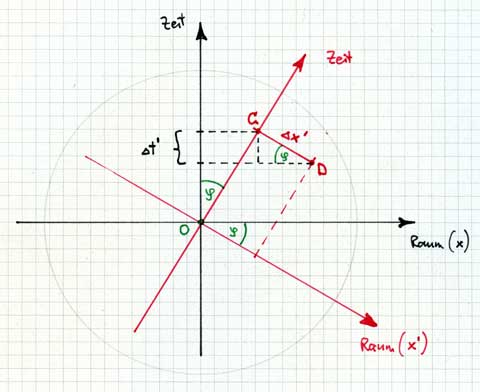
Schwarz stellt fest: ∆t’·c = ∆x’·sin(φ) = ∆x’·v/c , das ist bis aufs Vorzeichen die Formel von B6 ! Aber auch das Vorzeichen können wir ablesen: Die vordere Uhr von Rot geht aus der Sicht von Schwarz nach. Es muss also heissen ∆t’·c = –∆x’·sin(φ) = –∆x’·v/c in vollkommener Übereinstimmung mit B6.
Es ist eine lohnende (also auch nicht ganz einfache) Aufgabe sich zu überlegen, wie der Versuch, vorbeifliegende distante Uhren wie in B6 zu synchronisieren, im Epstein-Diagramm aussieht. Man muss dabei beachten, dass sich Licht in jedem Bezugssystem immer mit c bewegt, dass also der Quotient v/c für Licht 1 ist und damit der Winkel φ immer 90º beträgt! Licht bewegt sich in jedem Bezugssystem nur räumlich, parallel zur Raumachse. Und: Photonen altern nicht!


