D5 Quergeschwindigkeiten und Aberration
Wie stellt es sich eigentlich für Schwarz dar, wenn sich im roten System ein Objekt mit einer Geschwindigkeit u’ quer zur Relativgeschwindigkeit v bewegt ? Bis jetzt haben wir nur Bewegungen entlang der x-Achse betrachtet.
Für die Herleitung der Transformation einer solchen ‘Quergeschwindigkeit’ brauchen wir die Lorentz-Transformationen nicht. Die Kenntnisse der Grundphänomene genügen dafür völlig. Es sei also u’ eine Geschwindigkeit z.B. in der y’-Richtung von Rot. Dann gilt
u’ = ∆y’ / ∆t’ = ∆y / ∆t’ = ∆y / ( ∆t · √ ) = ( ∆y / ∆t ) / √ = u / √
Schwarz misst also die kleinere Quergeschwindigkeit u = u’ · √
Dieses Resultat werden wir in E1 noch brauchen. Wir verwenden es hier noch zur Herleitung der korrekten Formel für die Aberration. Unter der Aberration (lat. aberrare ~ abirren, abweichen) versteht man die Richtungsänderung von Geschwindigkeiten, die sich dadurch ergeben, dass sich der Betrachter ebenfalls bewegt. James Bradley hat 1728 erkannt, dass die winzigen jährlich-periodischen Positionsverschiebungen von Fixsternen als Folge der Bewegung der Erde um die Sonne zu verstehen sind. Der Legende nach wurde ihm das klar, als er bei Windstille und englischem Regen in der Kutsche fuhr und dabei beobachtete, dass der Regen umso schräger zu fallen schien, je schneller die Kutsche fuhr.
Betrachten wir ein Fernrohr, welches in eine Richtung zeige, die senkrecht zur momentanen Fahrtrichtung der Erde auf ihrer Umlaufbahn steht:
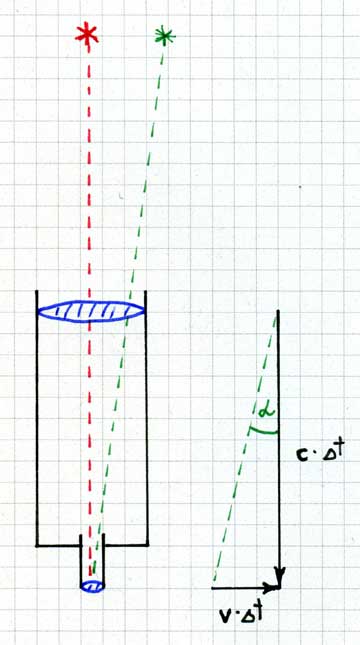
In der Zeit, die das Licht eines Sternes braucht, um vom Objektiv bis zum Okular zu gelangen, ist die Erde schon ein Stück auf ihrer Bahn vorangekommen. Wir müssen daher das Teleskop um einen Winkel α abkippen, damit der Stern in die Mitte des Gesichtsfeldes abgebildet wird. Um diesen Winkel ‘irrt also der Lichtstrahl ab’ infolge der Bewegung der Erde. Die hergebrachte Formel für diese Aberration ist tan(α) = v/c , wo v die Geschwindigkeit der Erde auf ihrer Umlaufbahn ist (das sind fast 30 km/s). Der Winkel hat eine Grösse von etwa 20 Bogensekunden.
Einstein hat schon 1905 darauf aufmerksam gemacht, dass diese traditionelle Formel nur näherungsweise richtig ist. Quergeschwindigkeiten sind nach obiger Formel zu transformieren, und es ergibt sich dann die korrekte Formel tan(α) = v / ( u’·√ ) = v / ( c·√ ) . Diese Formel erhält man auch, wenn man in der obigen Figur den vom Licht zurückgelegten Weg korrekterweise der Hypotenuse zuordnet statt der Kathete. Für die Quergeschwindigkeit u des Lichts liefert dann der Pythagoras u = c·√ , womit man für den Wert von tan (α) wieder v / u = v / ( c·√ ) erhält. Für Licht gilt also exakt die neue Aberrationsformel sin(α) = v/c . Diese Korrektur ist astronomisch natürlich unbedeutend, die Werte der Sinusfunktion und der Tangensfunktion unterscheiden sich ja für kleine Winkel kaum.
Wir könnten jetzt ohne weiteres auch den allgemeinen Fall betrachten, wo sich im roten System ein Objekt mit einer beliebigen Geschwindigkeit w’ + u’ in eine beliebige Richtung bewegt. Schon in der Originalpublikation von 1905 handelt Einstein diesen Fall ab [12-158f] und gibt für die resultierenden Geschwindigkeiten und Winkel im schwarzen System schöne symmetrische Formeln an. Ebenso wird auch die Aberration ganz allgemein behandelt. Die entsprechenden Rechnungen sollten jetzt für den Leser gut nachvollziehbar sein. Wir werden diese Resultate im folgenden aber nicht brauchen. Einige Hinweise dazu finden sich noch in K3.


